K-Nearest Neighbor algorithms (KNN)

如果我們有一筆資料 $(x_1,y_1),...,(x_n,y_n)$，

且 $x_i \in \mathbb{R}^2, y_i \in {0,1}$ (即 $x_i=(x_1,x_2)$為二維的自變項以及 $y_i = 0 ~or~ 1$的依變項)。如圖所示：

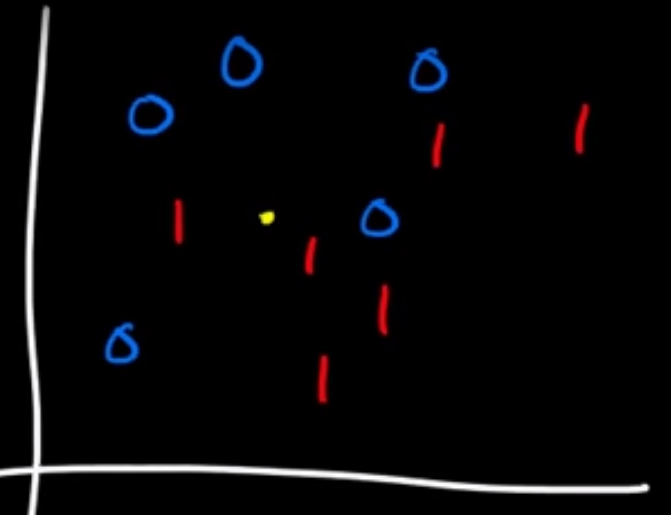
橫軸為 $x_1$、縱軸為 $x_2$、藍色和紅色分別為已知的分類(0或1)。圖中的黃點並非髒污，而是要進行分類的 $x$。

KNN的概念其實很就是去算點與點之間的距離，距離越近表示類型越像(和K-means有異曲同工之妙，但注意，KNN是屬於Supervised learning，這點和K-means不同)。 若 $k=1$，則是根據離黃點最近的「1個點」之分類為分類; $k=3$則是根據離黃點最近的「3個點」之分類為分類並採取多數決(majority vote of k nearest)。以下圖為例：

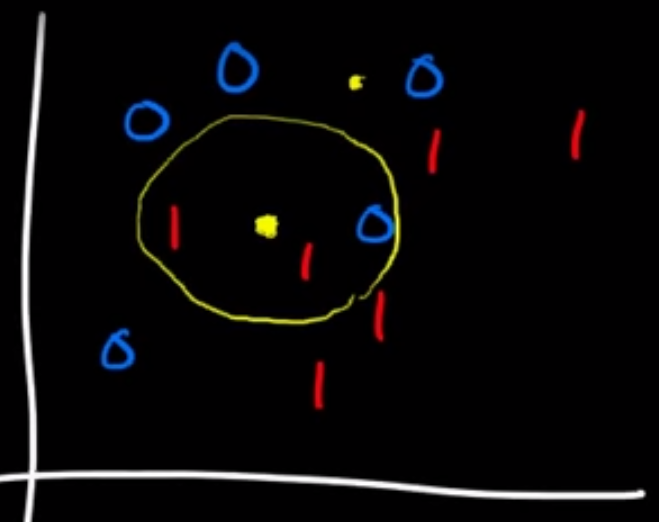
此例為 $k=3$，意即離黃點最近的三個點分別為1,1,0的分類，依照多數決應將黃點分類為類別1。

若將KNN寫成公式的話：

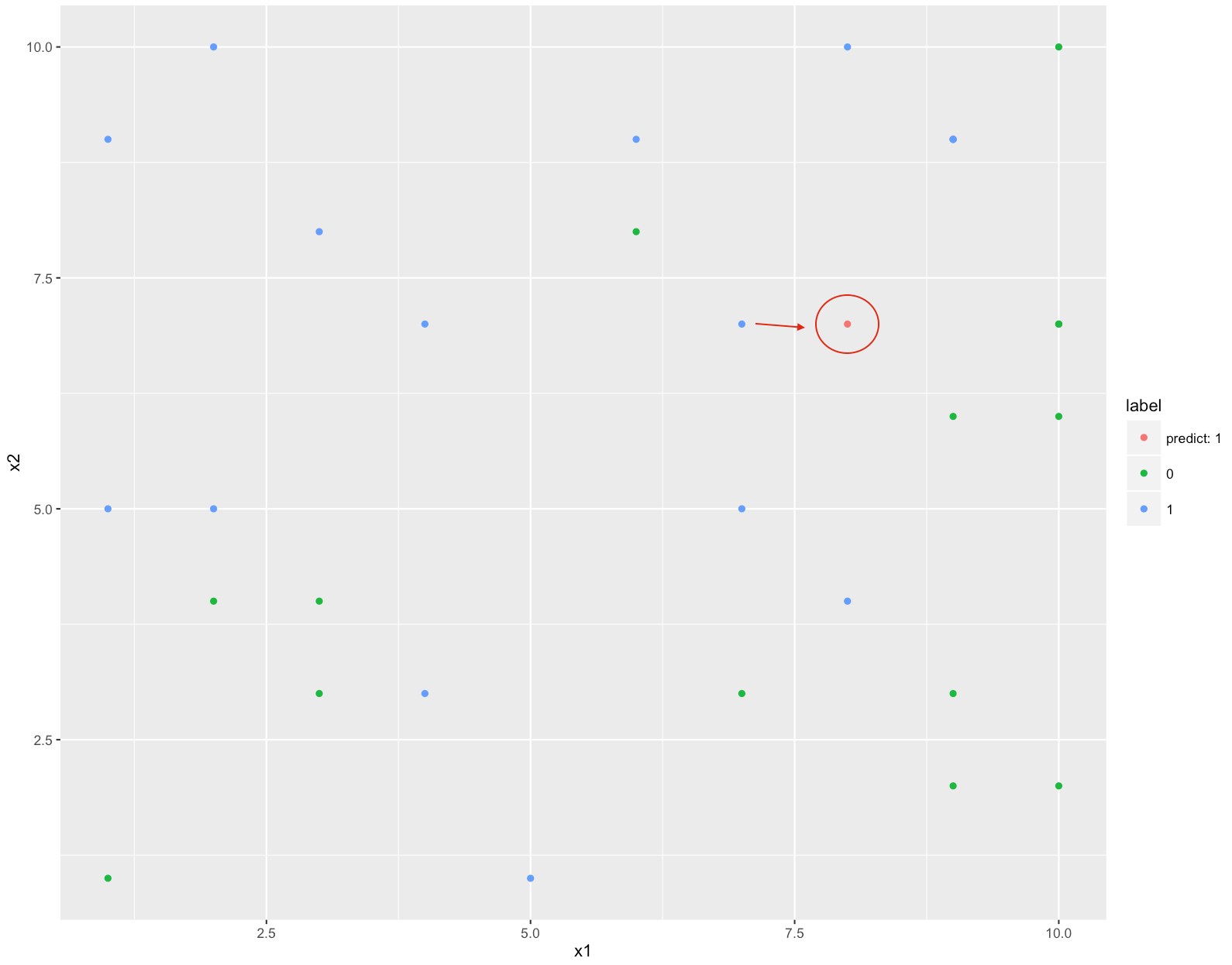
此為 $k=1$的例子，已知紅點距離最近的點為藍色，因此判斷紅色的分類為1。有興趣的話可以參考下列R code。可以自己調整參數玩玩看

# K-Nearest Neighbor classification ---------------------------------------
library(data.table)
library(ggplot2)
#training data
#simplify to two-dimensional real numbers
dt <- data.table(x1=sample(1:10,30,replace=T),x2=sample(1:10,30,replace=T),label=as.factor(sample(0:1,30,replace=T)))

#new x^(2)=(x1,x2)
newX=c(8,7)
k=1 #k could be a odd number

#find out the label of k smallest distances of x
nearestLabels <- dt$label[!is.na(match(sqrt((newX[1]-dt$x1)^2+(newX[2]-dt$x2)^2),sort(sqrt((newX[1]-dt$x1)^2+(newX[2]-dt$x2)^2))[1:k]))]

#majority vote of k nearest points
tb <- as.data.table(table(nearestLabels))
predictLabel <- paste("predict: ",tb$nearestLabels[match(max(tb$N),tb$N)],sep='')
predict.dt <- data.table(x1=newX[1],x2=newX[2],label=predictLabel)

#bind preditVal to original dt
dt <- rbind(predict.dt,dt)

#plot the outcome
qplot(x1,x2,colour=label,data=dt)