Decision, Regression tree

Decision tree 與 Regression tree的概念都是建一顆樹(e.g. binary tree, minimize the traning error in each leaf)且都是Supervised learning。差別在於資料形態的不同：

• Decision tree: $x_i \in \mathbb{R}, y_i \in $ { $ Finite~Set $ }$ $
• Regression tree: $x_i \in \mathbb{R}, y_i \in \mathbb{R}$

Decision tree會有類別變項：

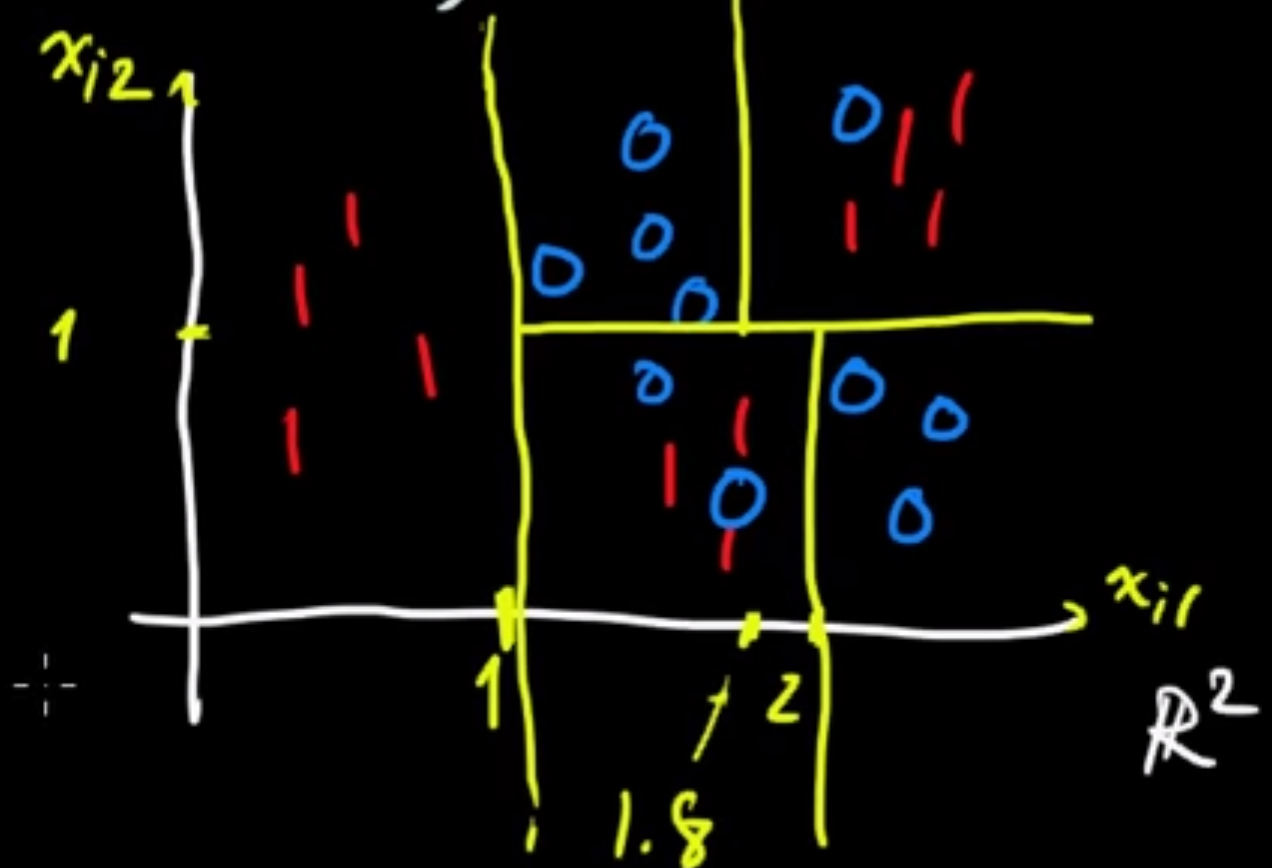
利用不斷的二分法將區域切出來。再依照該區的類別採多數決(majority vote of classification)進行分類。如下圖：

但因為採多數決，所以會有區域誤判的可能(下文會提到Impurity Measures來衡量誤判率)。

先前提到Regression tree 和 Decision tree的差別為資料形態的不同，最簡單的例子即 $x$, $y$ 皆為實數。實際做法會先將 $x$切出好幾個區域(為決策的判斷)，接著在各個區域內得出預測值
$\hat{y}$， 此預測值是來自該區依最小平方法得到的: $\bar{y} = min\sum_{i \in \mathbb{R}_k}(\hat{y}-y_i)^2$，即該區的平均值：

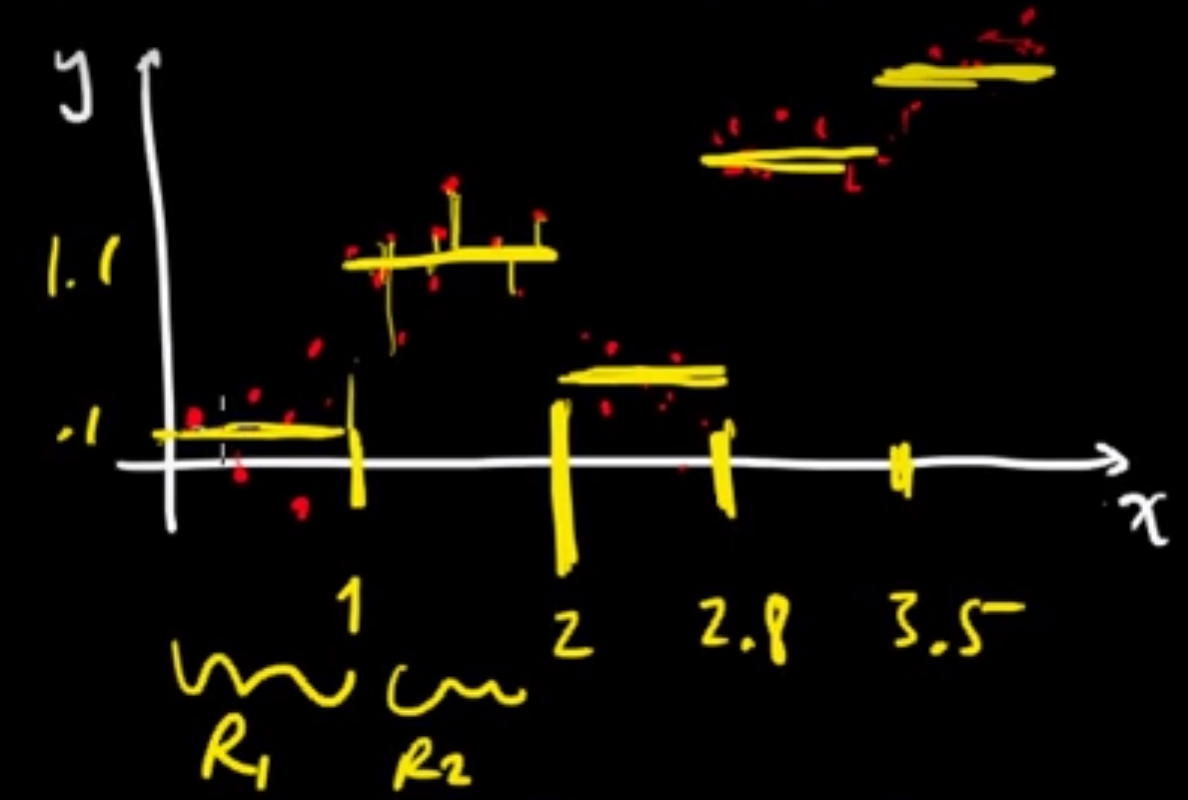
因此得到的預測值 $y$ 即為該區的 $\bar{y}$：

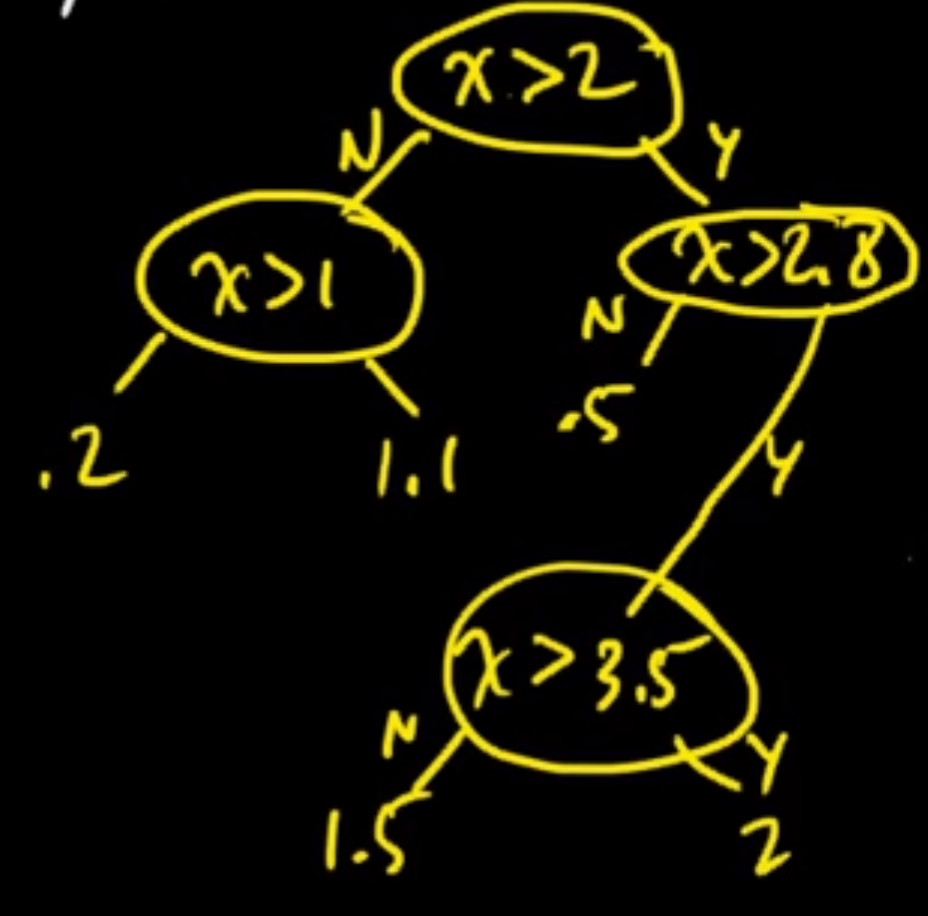
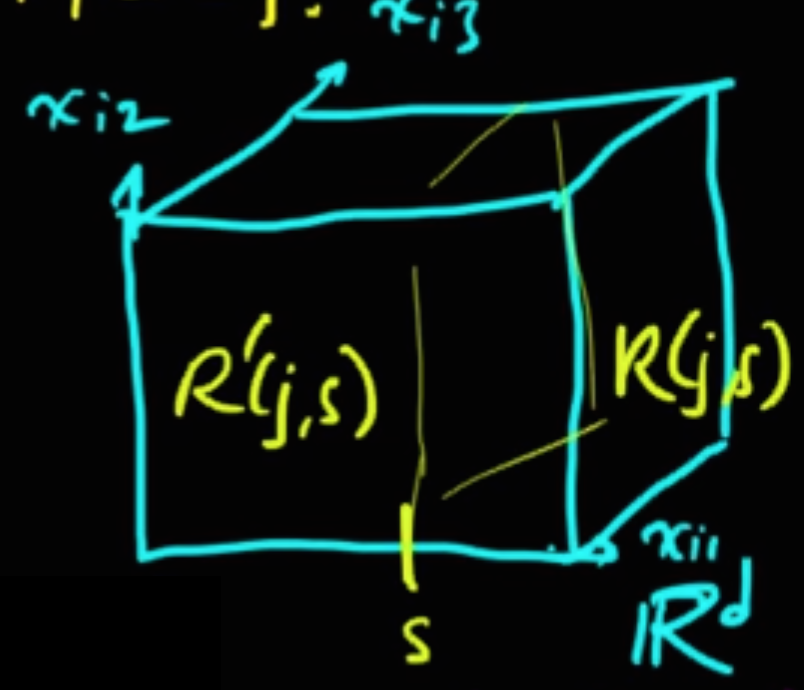
那我們要如何擴充樹葉呢(也就是圖中的每個節點)? 以三維空間舉例：

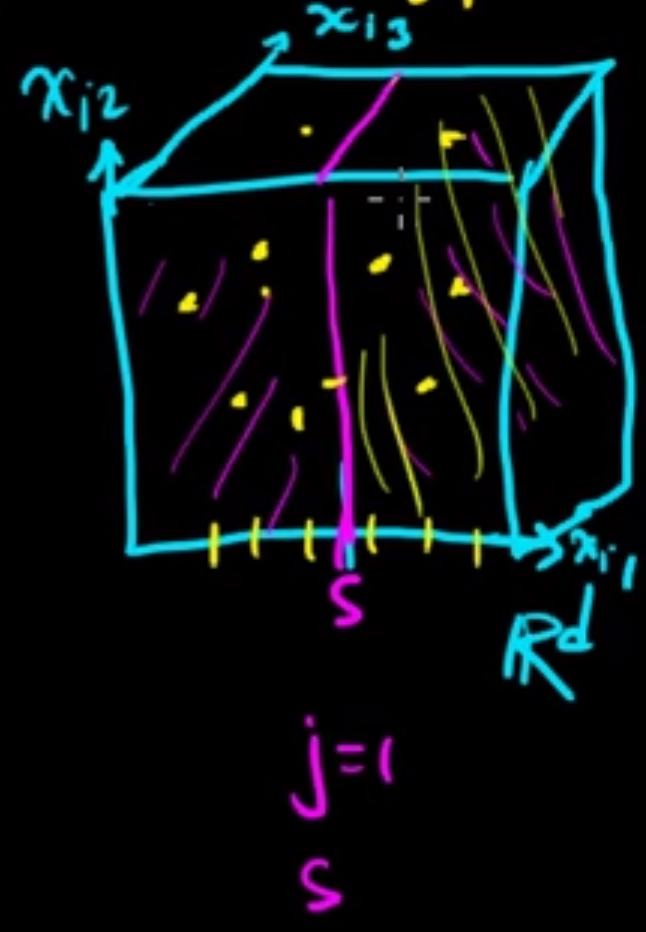
如果要長regression tree，首先選定一個維度 $j=1$，根據資料點找出點 $s$ 使得 $ \sum_{x_{ij}>s,x_i \in \mathbb{R}_j}(\hat{y}-y_i)^2$

加上

$\sum_{x_{ij} \leq s,x_i \in \mathbb{R}_j}(\hat{y}-y_i)^2$最小，根據這個原則重複步驟就可以做出一堆的sub-region。
那到底要切到何時呢?有兩種標準：

• Stop when one points in the (sub-)region
• Only consider splits resulting in the (sub-)region with $\geq 5$

同理，要長decision(classification) tree也是依照類似的方法，以二維平面解釋：

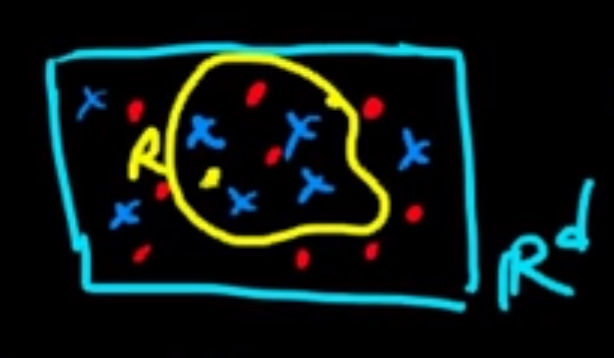
先定義一下，$E_R$: misclassified by a majority vote in the (sub-)region，以此圖為1/3，算法為 $min \frac{1}{N_{R_j}}\sum_{x_i \in \mathbb{R}_j} I(y_i \neq y) ,~y= ~${$ Finite~Set $}$, N_R=~ ${$ i:x_i \in \mathbb{R_j} $}

若以三維空間說明的話，則是讓切出的兩區的 $E_{R_j}(j,s)+E_{R_j}'(j,s)$ 最小化：

Impurity Measures

前述提到分類誤判，衡量一個模型的分類誤判率有三種常見的方式：

• $E_R$: $P_R(Y), ~Y= ~${$ Classification Finite~Set $}
• $H_R$ (Entropy): $-\sum_{y \in Y}(P_R(Y) \cdot \log{P_R(Y)})$
• $G_R$ (Gini's index): $\sum_{y \in Y}(P_R(Y) \cdot (1-P_R(Y)))$